Tail call과 Tail recursion

꼬리 물기 최적화라고 합니다. 여러 블로그를 구경하다가 알게된 개념이었고, 알고리즘 문제 해결을 좋아하셔서 runtime 시간 최소화를 신경써야 하는 경우에 필수적으로 알아두어야 합니다.

지연 평가 (lazy evaluation)

느긋한 계산법(Lazy evaluation)은 계산의 결과값이 필요할 때까지 계산을 늦추는 기법이다 ... 느긋하게 계산하면 필요없는 계산을 하지 않으므로 실행을 더 빠르게 할 수 있고, 복합 수식을 계산할 때 오류 상태를 피할 수 있고, 무한 자료 구조를 쓸 수 있고, 미리 정의된 것을 이용하지 않고 보통 함수로 제어 구조를 정의할 수 있다. - wiki

여러 이점이 있지만 불필요한 계산 안함 이라는 이점이 제일 가시적입니다.

엄격한 평가(strict evaluation)

지연 평가의 반대인 엄격한 평가는 우리가 일반적으로 사용하는 use case 입니다.

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ....10000]
  .filter((_, index) => index % 2 === 0)
  .map(v => v * 10)
  .slice(0, 2);

위와 같은 chaining 연산은 filter가 25000번, map이 25000번, slice가 2번 돌게 됩니다. 코드는 간단하게 만들었지만 50002번이나 도는 엄청난 병목이 생기는 지점을 만들어냈습니다. 조금 만 더 생각을 해본다면 아래처럼 고칠 수 있겠죠.

// 결과가 단계마다 값 별로 생겨남
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ....10000]
  .slice(0, 4) // [1, 2, 3, 4]
  .filter((_, index) => index % 2 === 0) // [2, 4]
  .map(v => v * 10); // [20, 40]

slice 4, filter 4, map 2, 총 10번의 반복으로 종료됩니다.

이러한 지연 평가 함수를 항상 고려하고, 순서를 바꿀 수 없는 상황 등의 이유로 임의로 만들기란 쉽지 않습니다. 그래서 보통 lodash를 이용해 많이 만들곤 합니다.

// 결과가 단계마다 실행 함수 별로 생겨남
const arr = [0, 1, 2, 3, 4, 5]
const result = _.chain(arr) // lodash에서 chain으로 묶으면 지연 평가 대상이 되고, 이후 value로 값을 꺼내 사용할 수 있음.
  .filter(num => num % 2 === 0)
  .map(num => num + 10)
  .take(2)
  .value();

// chain (0) -> filter (true) -> map (10) -> take (success, 10)
// chain (1) -> filter (false)
// chain (2) -> filter (true) -> map (12) -> take (success, 12)
// chain (3) -> filter (false)
// chain (4) -> filter (true) -> map (14) -> take (fail)
// chain (5) -> filter (false)
// chain (6) -> filter (true) -> map (16) -> take (fail)
....

최종적으로는 결과값이 필요한 2개의 지연 평가 부분을 제외하고는 연산이 실행되지 않습니다.

지연 연산

지연 평가는 tail recursion 을 하는데 필요한 내용은 아니지만, 지연 연산에 대한 개념을 위해 정리해봤습니다. 지연 연산은 지연 평가에서 연산을 바로 하지 않고 실제 실행이 되는 시점에 진행하는 것인데요, 연산자 만으로 지연 연산을 할 수 있도록 도와주는 연사자들이 있습니다. ||, &&, 삼항연산자 이 3가지 입니다.

이 3가지 외의 연산을 사용하게 되면 연산들이 stack에 쌓이게 됩니다.

Tail call

함수는 기본적으로 호출 후, 완료됐을 때 호출한 부분으로 돌아가기 위해 이전 공간을 stack에 쌓아둡니다. 그 이유는 마저 할 일이 남아있기 때문입니다.

const  fibo = (n) => {
  if (n < 2) {
    return n;
  }
  return fibo(n - 1) + fibo(n - 2);
}

n에 5를 넣었을 때 실행 컨텍스트의 순서는 어떻게 될까요?

fibo(5)
  fibo(4)
    fibo(3)
      fibo(2)
        fibo(1)
          1
        fibo(0)
          0
      fibo(1)
        1
    fibo(2)
      fibo(1)
        1
      fibo(0)
        0
  fibo(3)
    fibo(2)
      fibo(1)
        1
      fibo(0)
        0
    fibo(1)
      1

최대 depth는 5개가 됩니다. 만약 이 depth가 1000개, 100000개가 된다면 어떻게 될까요...?? 그렇기 때문에 마저 할 일을 없애서 원래 자리를 stack에 쌓지 않도록 하는 방법이 tail call 입니다.

Tail call optimize

함수가 return에서 호출된 뒤, 돌아왔을 때 아무런 할 일이 없으면 됩니다. 별도의 변수에 결과를 받아 return 하는 것 조차 할 일이 되므로 return에서 함수를 호출해줘야 합니다.

// 1번
const a = () => {
    let b = 0;
    return test(--b);
}

// 2번
const a = () => {
    let b = 0;
    return test(b--);
}

둘 중 어떤 것이 tail call이 될까요? 답은 1번입니다. 2번은 다음 라인에서 1이 빼지기 때문. 결국 함수 호출 이후가 되기 때문에 stack에 메모리가 쌓이게 됩니다.

tail call 방식은 stack을 쌓지 않고 재사용 하는 방식으로 언어 level로 지원하기도 합니다. 물론 js도 지원하지만 브라우저는 현재 ios만 지원하고 있는 상황입니다.

Tail recursion

tail recursion은 tail call로 자기 자신의 함수를 호출하는 것을 말합니다.

const fibo = (n, prevFibo = 1, pprevFibo = 0) {
  let temp;
  temp = prevFibo + pprevFibo;
  pprevFibo = prevFibo;
  prevFibo = temp;

  return n < 3 ? prevFibo : fibo(n - 1, prevFibo, pprevFibo);
}

그렇다면 처음에 만들었던 fibo함수와 비교해보겠습니다.

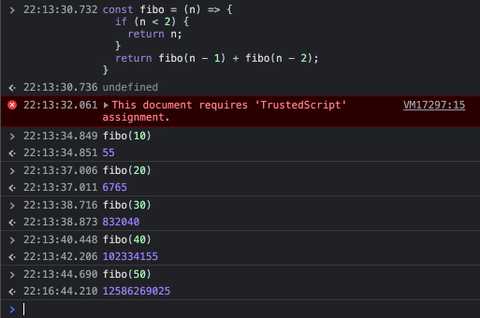
우선 일반 fibo함수입니다.

fibo(40)을 하니 1.8s이 걸리고, fibo(50)을 하니 브라우저가 멈춥니다...! 계속 기다려보니 약 3분뒤 성공했습니다.

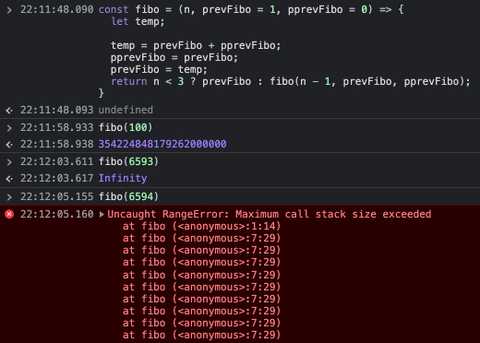
후...! 과연 tail recursion fibo함수는 어떨까요?

fibo(100)의 결과가 0.005s 소요됩니다. maximum call stack size 직전까지 사용하는 fibo(6593)은 0.006s 소요됩니다.

마무리

메모리 문제는 알고리즘에서 특히 많이 신경써야 하지만 비단 알고리즘 뿐만 아니라 실전인 서비스 코드에서 더 많이 신경써야 합니다. 간단한 api call과 데이터 맵핑만 하던 일상에서도 이러한 최적화 기법들을 잊지 말아야 합니다.